論理学の試験ではシーケント計算を使おう！という話(+Coqの紹介)

アドベントカレンダー2025

2025-12-21

はじめに

どうも。論理学のテストで普通に苦戦してしまったキリンです。初めてのアドベントカレンダー、はて何を書こうか…と思いましたが、講義で論理学の考え方を教えてもらうだけではあんな問題解けないだろ！と思い、どうすればよいのかと試行錯誤したことを書き出してみました。拙い文章ですが良ければ読んでいってください。

規則(演算子)に順序をつけて順番に処理していくという考え方

高校数学などで扱った整式の記号には処理すべき順番が存在します。例えば次の整式

2x^2 + 3 = x(x+3^2 - 5)

を $x$ についての2次方程式の標準的な形 $ax^2+bx+c = 0$ に変形して解を求めるまでの過程を詳しく書くと(ここではわかりやすさの都合上、解の公式ではなく因数分解を使用する)、

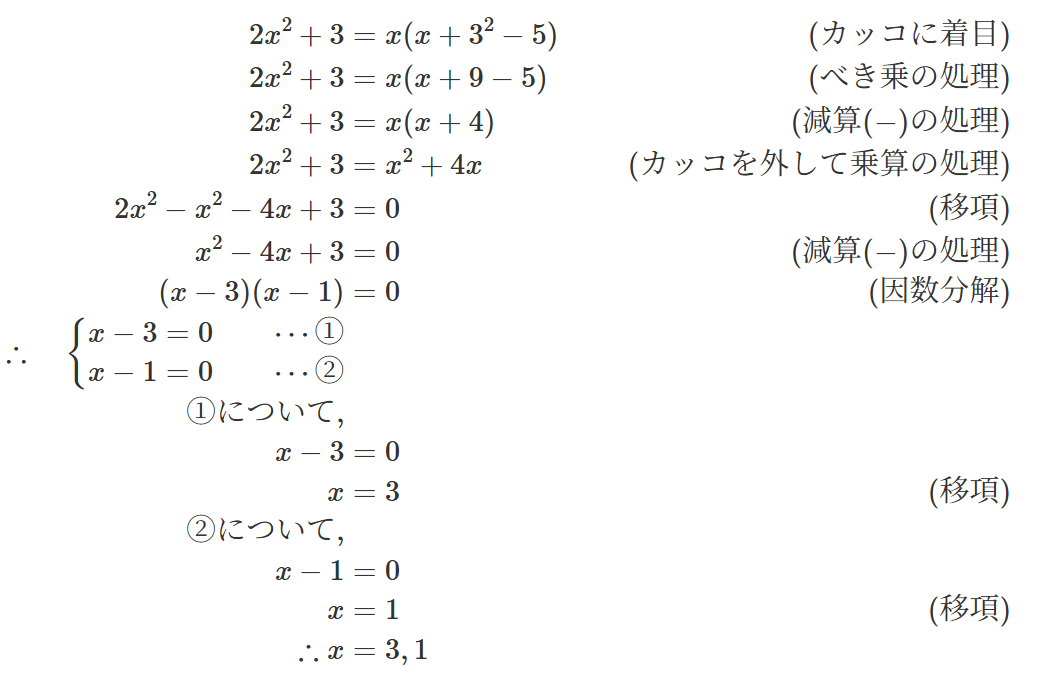
もちろん問題によってはいくらでも楽に計算ができるやり方は存在するとおもいますが、一般的にはこのような問題は以下のような順序で皆さん解かれると思います。

右辺と左辺それぞれについて以下の順序で処理を行う
移項して同類項で加減算を行い、標準形 $ax^2 + bx + c = 0$ に変形
解の公式または因数分解を用いて解を導出

高校まではこのような計算を機械的に行う手順や方法を授業でたくさん教え込まれたにも関わらず、大学に入った瞬間残念ながらテスト対策のための問題演習などはあまり行われなくなってしまいました。にも関わらずテストでは具体的な計算問題を自力で解くことが求められます。論理学においても例外ではありません。一見しただけではとても意味のわからない証明木を自力で書かなければいけません。どうすればいいのでしょうか？実は上の2次方程式の例と似たような(？)感覚で古典論理の命題論理式の証明構成をシーケント計算によって行うことが(多分)できます。(古典論理やシーケント計算、自然演繹といった用語の詳しい説明は今回は省きます、すみません…)

シーケント計算のわかりやすい書き方

例として、古典論理の命題論理式 $\vdash (p \to q) \lor (q \to p)$ の証明の考え方を上の二次方程式の解の導出と似たような書き方で書くとこのようになります。

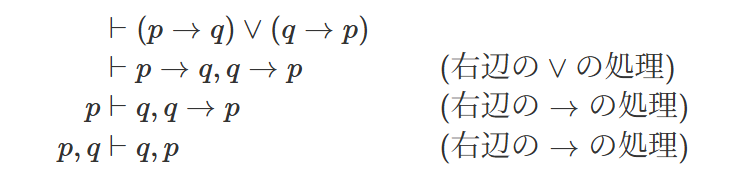
両辺に共通する原子論理式が少なくとも一つ存在すること(この場合は $p、q$ がともに両辺に存在する)を確認して証明完了です。

証明木にすると以下のようになります。

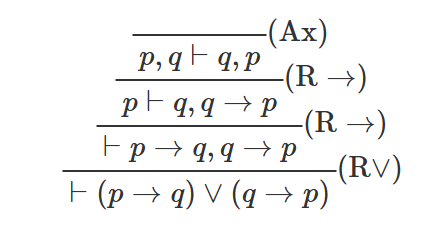
もう少し複雑な例として $p \to q \vdash (p \lor p) \to (r \to q)$ の証明も一応貼っておきます。

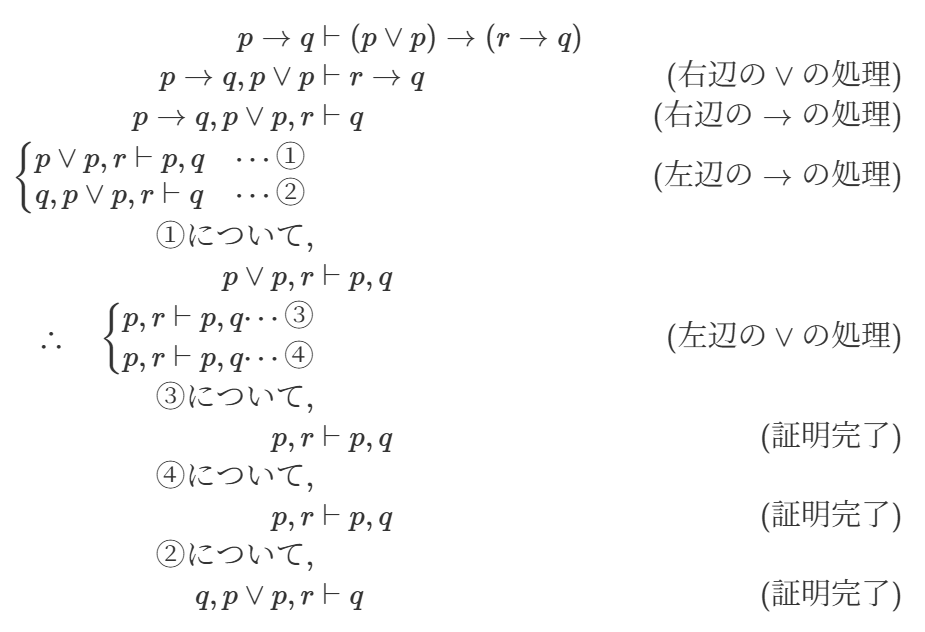
証明木は以下のようになります。

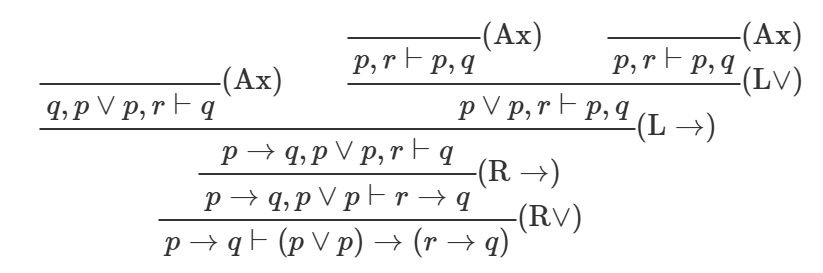
見ていただければ分かる通り、講義で学習するような証明木とは上下が逆になっていますが、機械的に証明を導出する際には逆から推論することが必要になります。それで具体的にどのような規則から処理していけばいいかというと、

両辺に共通の原子論理式があるかの確認
左辺の $\land$ 、右辺の $\to$ と $\lor$ の処理、 $\neg$ の処理 (分岐しない処理)
左辺の $\to$ と $\lor$ 、右辺の $\land$ の処理 (分岐する処理)

のように処理していけば良いらしく、実は結構単純です。講義で出てくるような単純な古典論理の命題論理式であればこの原則に従っていれば機械的に証明を構成できると思います(多分)。

自然演繹との比較

さっきの例で用いた命題論理式 $(p \to q) \lor (q \to p)$ を自然演繹で証明してみましょう。まずシーケント計算の証明木を書き下すと以下のようになります。

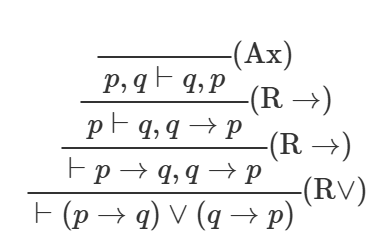
次に、これに対応する自然演繹の証明木は以下のようになります。

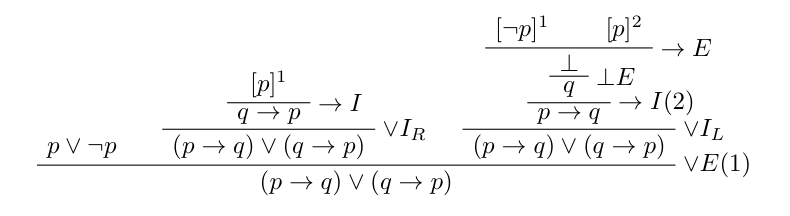
まず下から二段目で分かれているところの一番左の枝についてですが、これは排中律の導入を表しています。これによって $(p \to q) \lor (q \to p)$ を $p$ が真の場合と $p$ が偽の場合に場合分けしています。真ん中の枝は $p$ が真ということを仮定した場合で、このとき $(p \to q) \lor (q \to p)$ が真であるには $q \to p$ が真であればよく、 $p$ を仮定すればこれは成り立つ、という流れになります。右の枝は $p$ が偽と仮定した場合で、このときは仮定より $q \to p$ が真であることはありえないため、 $p \to q$ が真でなければなりませんが、これは $q$ が真であることを仮定しなければ成り立ちません。そこで爆発律(矛盾から任意の命題を導くこと)を利用して無理やり(?) $q$ を導く、という流れになっています。この2つの証明木を見比べて素朴に思うことがあるとすればおそらく、なぜシーケント計算の証明木は枝分かれしていないのに自然演繹ではわざわざ排中律を用いて枝別れさせているのだろうか、ということでしょう。これはなぜかといえば、(古典論理の)シーケント計算では結論(右辺)に複数の論理式を持つことができるのに対し、自然演繹では一つの枝に一つの論理式しか持つことが許されないからです。この例で言えば、シーケント計算では $p \to q、q \to p$ と書いて $\lor$ を外すだけで良いところを自然演繹では常に $p \to q$ か $q \to p$ のどちらかが必ず成り立つということをそれぞれのケースごとに追っていかなければなりません。自然演繹で証明を行う場合の考え方が、シーケント計算で行った場合より明らかに複雑になっていることがおわかりいただけたでしょうか。実際、自然演繹の証明を機械的に構成するのは難しいらしく、機械的に構成するには、シーケント計算の証明を構成したあとそれをアルゴリズムにより自然演繹に変換する、といった方法が主流らしいです。変換アルゴリズムはかなり複雑らしいので細かいところまで調べたい人は参考文献に上げた資料を参照してください。(自分は読んでませんが)

ちょっと紹介すると、大雑把に言えばシーケント計算の規則と自然演繹の規則はそれぞれ以下のように対応するらしいです。

公理 $\leftrightarrow$ 仮定
右規則(右辺の処理) $\leftrightarrow$ 導入則
左規則(左辺の処理) $\leftrightarrow$ 除去則

Coq(Rocq)をまじで軽く紹介

このままだと数学だけで技術要素がなくなってしまうので、直観主義論理の証明支援系であるCoq(現:Rocq)をまじーーーーーーーーーーで軽く紹介してみます。自分は正直エディタの使い方も文法もあまりわかっていません(ちゃんと紹介するには自分のような超初学者にはあまりにも奥が深すぎる)

インストール

Linux(UbuntuなどのDebian系)

sudo apt update && sudo apt install coq coqide

Mac

brew --cask install coq-platform

Windows

上の公式サイトにてインストーラーをダウンロード(Linux、Macでも可能)

https://rocq-prover.org/install#windows-vscode

その他、プログラミング言語OCamlのパッケージマネージャであるopamを使用してインストールする方法もあります。(こっちのほうがパッケージ管理の観点からは良いかもしれない)

https://opam.ocaml.org/doc/Install.html

証明例

先程の自然演繹の証明木です。

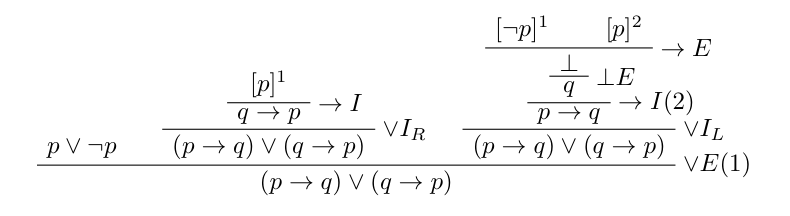
この証明をCoqで書くとこうなります。(注:厳密には $\forall p\forall q (p \to q) \lor (q \to p)$ を証明しています)細かい解説は知識に自信がないので省きます。

(* Coqのデフォルトは直観主義論理と呼ばれる古典論理とは性質が異なるものらしいので,古典論理の論理式の証明(排中律や背理法などを用いる必要がある証明)を行うにはライブラリをインポートしなければならない. *)
Require Import Coq.Logic.Classical.

Theorem classical_implication_or : forall P Q : Prop, (P -> Q) \\/ (Q -> P).
Proof.
  intros P Q. (* 全称量化子を除去*)

  destruct (classic P) as [HP | HnP]. (* 排中律(P \\/ ~P)によりゴール(証明目標)を Q -> P と P -> Q に分割*)

  - (* P が真 (HP: P) の場合 *)
    (* 右側の (Q -> P) が成り立つ *)
    right.
    intro HQ. (* ゴール(証明目標)は Q -> P からPになる *)
    apply HP.

  - (* P が偽 (HnP: ~P) の場合 *)
    (* 左側の (P -> Q) が成り立つ*)
    left.
    intro HP_contra.(* ゴールはP -> Q からQになる *)
    apply HnP in HP_contra.(* HnP は "P -> False" なので、HP_contra (P) を適用すると False になる *)
    destruct HP_contra.(* HP_contra は False になっており,"偽" からは任意の命題(ここでのゴールであるQも含む)が導けるため,証明完了 *)
Qed.

最後に

この記事を通して結局何が一番言いたかったかというと、シーケント計算を使って証明をしたほうが試験では多分楽だよ！ということです笑。この記事を見て試験勉強で楽できる人が一人でも増えていただければ幸いです。 (一階述語論理のシーケント計算についても紹介しようとしましたが、時間がないのと知識に対する自信がなかったので今回はなしということで許してください)