
はじめに
こんにちは!jackアドベントカレンダー 10日目の記事を担当します。リュカです。 この記事では、Blender のジオメトリノードを使ってレイマーチを再現したいと思います。
レイマーチとは
レイマーチとは3DCGの手法の一つで、目に届く光の経路を逆向きにトレースすることによって見えている画像をシミュレートするための手法です。 コンピュータで3Dを表現する際よく使われる手法は物体をポリゴンで表現するラスタライズ法ですが、形の正確さにおいてはレイマーチの方が優れています。
例えば、ラスタライズ法では球といった基本的形状であっても多面体で近似せざるを得ないのに対し、レイマーチでは計算精度の限り正確な形状を描くことができます。
本来はシェーダーで実装されることが多いのですが、レイマーチをBlenderの中で実現できればその強力な機能を利用できるため今回はBlenderを使うことにします。
作例の紹介
今回紹介する方法を使うと、以下のような映像を作ることができます。
環境
Blender:5.0.0
レイマーチの仕組み
先ほど、レイマーチが「光の経路を逆向きにたどる計算手法」だという話をしました。 ここではもう少しだけ踏み込んで、
- ポリゴンを使わず立体をどうやって表すのか
- 光の経路のトレースをどのように行うのか
について簡単に説明します。
距離関数
レイマーチでは、立体の形を直接ポリゴンで持つのではなく、代わりに ある点 p を受け取って「そこから一番近い物体までの距離 d」を返す関数によって表現します。 これを 距離関数(distance function) と呼びます。
例えば、原点中心・半径 r の球なら、距離関数は
float d_sphere(vec3 p){
float r = 1.0; // 球の半径
return length(p) - r;
}となります。立体に埋まっている点に対しては負の値を返すようにします。
レイマーチのアルゴリズム
光線の先端から立体の表面までの距離を計算して、その分だけ光線を進めることを繰り返します。 コードで表すとこんな感じです。
const int MAX_STEPS = 128;
const float EPSILON = 0.001;
const float MAX_DIST = 100.0;
float raymarch(vec3 origin, vec3 dir) {
vec3 pos = origin;
float dist = 0.0; // origin からどれだけ進んだか
for (int i = 0; i < MAX_STEPS; i++) {
float d = distanceToScene(pos);
pos += dir * d; // 距離 d だけ前に進める
dist += d;
if (d < EPSILON) {
return dist; // 立体表面に到達
}
if (dist > MAX_DIST) {
break; // 背景に到達
}
}
return dist;
}光の到達地点が分かれば物体の色、光源からの光の当たり方、影等々を計算してその方向に見えている色を計算できます。 これが画像の一ピクセルに相当するため、すべてのピクセルに対して同じ計算をすれば画像が得られるというわけです。
Blender でレイマーチを再現する
いよいよBlender上で実際に作っていきます。
シーン準備
新しいシーンに最初から置かれているCubeを選択し、ジオメトリノードタブを開きます。 「New」をクリックして新規ノードツリーを追加します。名前はRaymarchとでもしておきましょう。
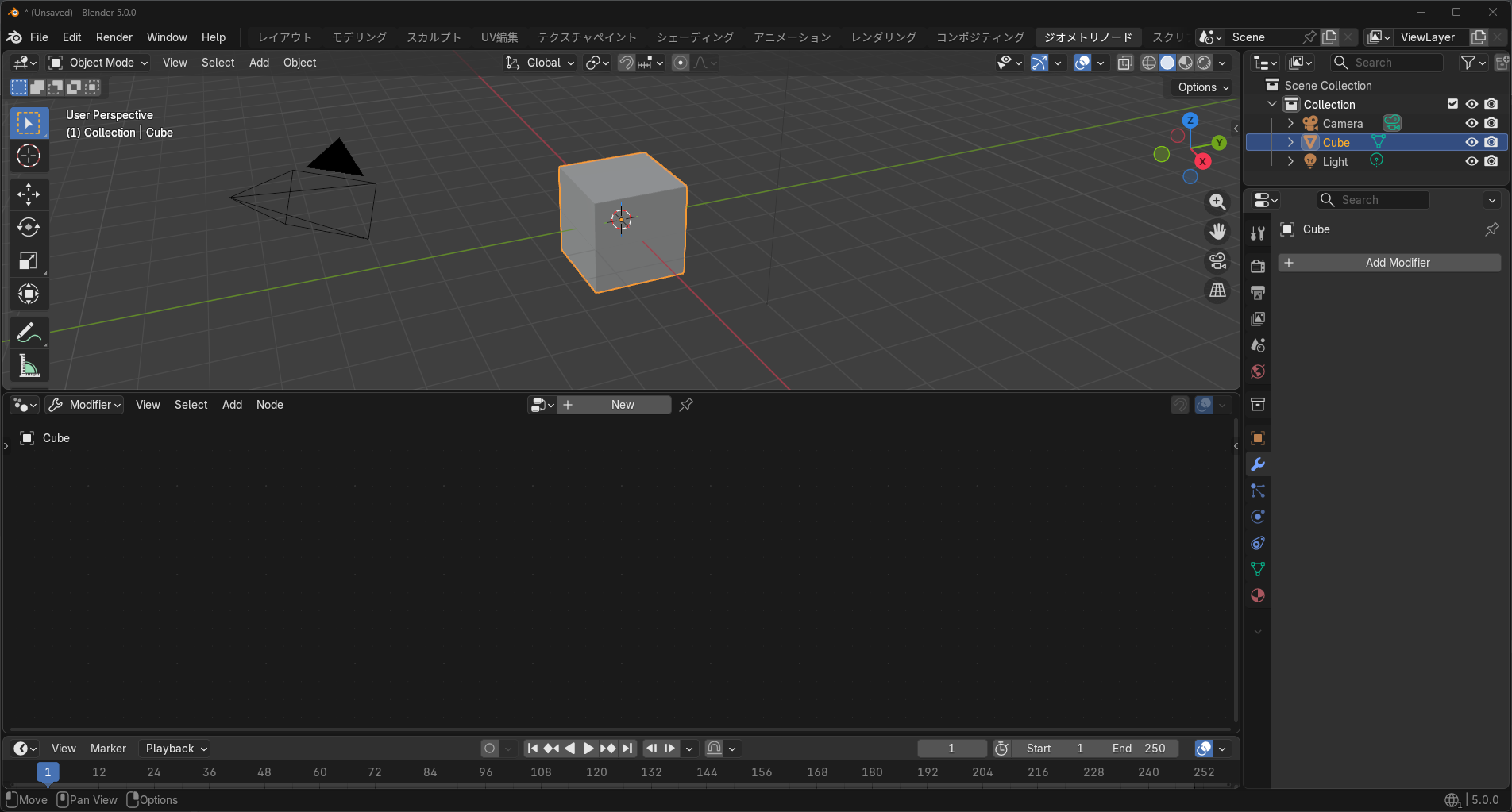
グリッドの追加
Blenderで立体を描画するためには最終的にはポリゴンになっている必要があるため、頂点をレイの代わりに動かすことにします。
Gridノードで頂点を用意し、ObjectInfoノードで参照したカメラの位置情報をもとに頂点をカメラの前に配置しています。
Outputの設定から解像度をグリッドに合わせて1024px×1024pxに変更します。
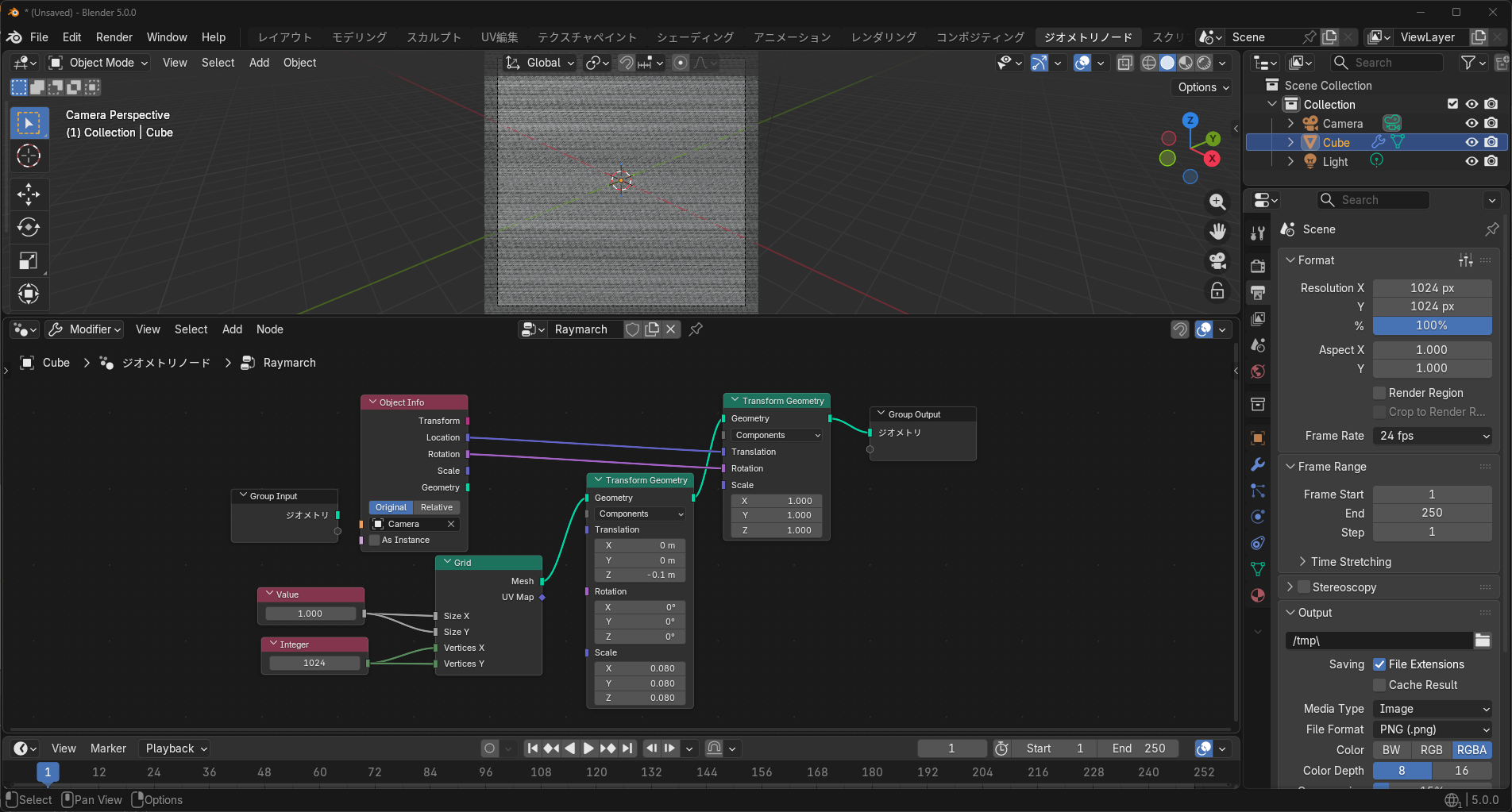
レイ方向の定義
Store Named Attribute ノードで新しい変数 ray_direction を定義します。レイの方向を表す変数で、これは視点とグリッドの座標の差を正規化することによって得られます。(選択したノードが新たに追加されたノードです)(以下同様)
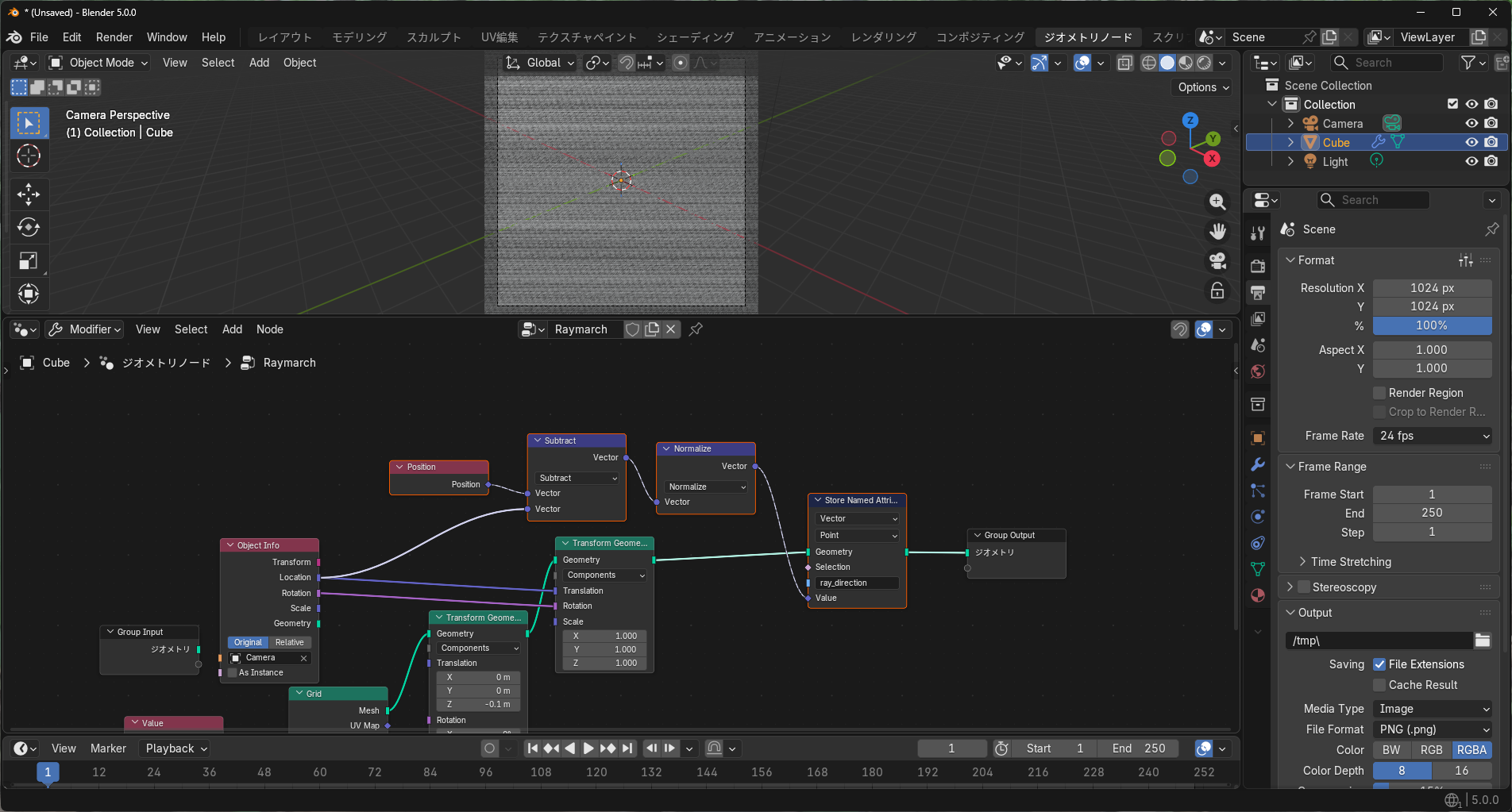
レイマーチループの定義
Simulationノードで頂点位置の更新を繰り返します。
Position, Distance, Subtractノードが球の距離関数に対応し、距離関数の値に応じて ray_directionの方向に移動しています。
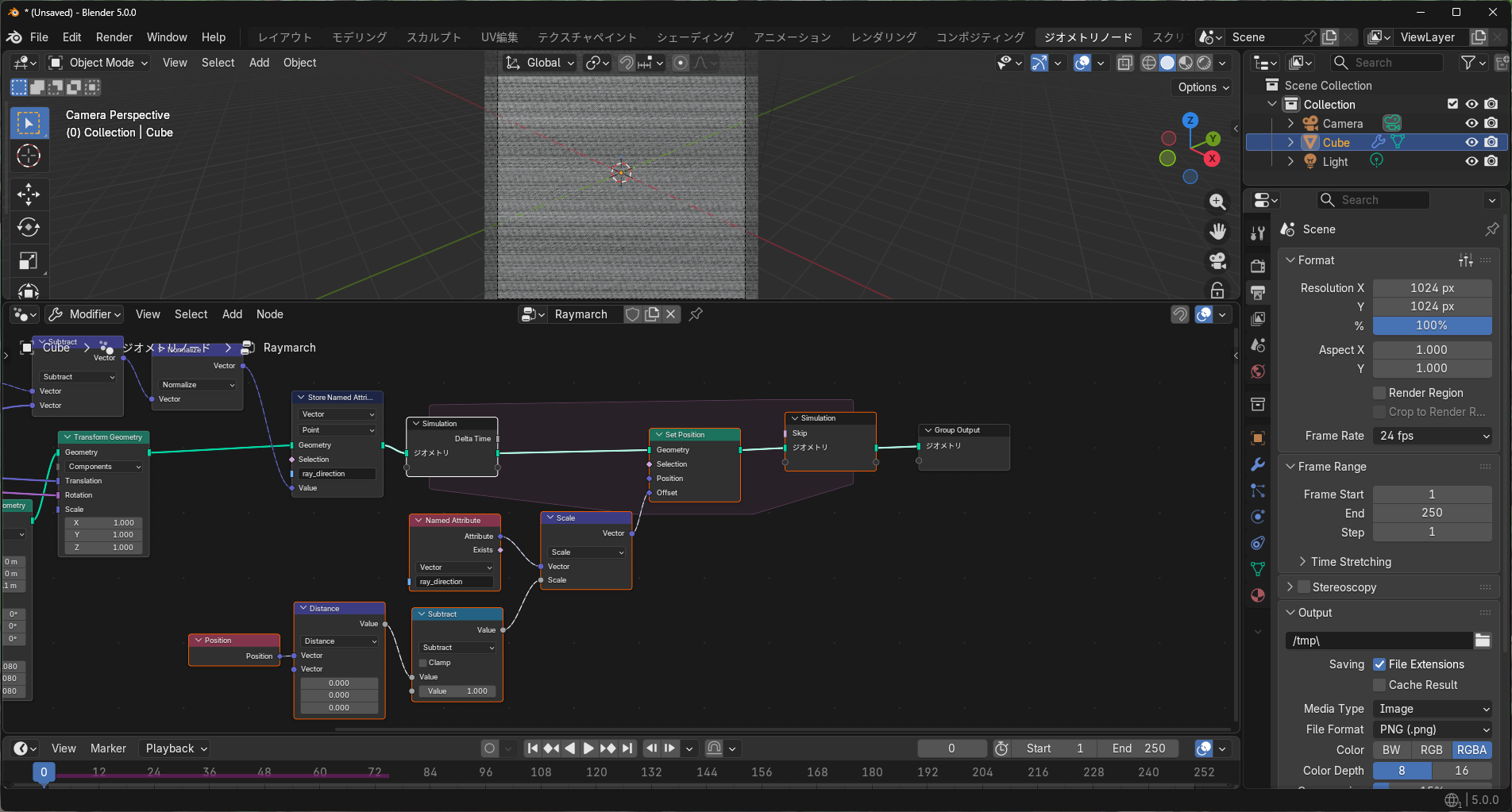
ここまでできたらフレームを再生してみましょう。視線方向に頂点が飛んでいって球が現れるのが分かります。カメラ方向以外から見ると球にぶつからなかった頂点が長く尾を引いています。
距離関数をもう少し複雑なものにしてみましょう。Wrapノードを使うと距離関数により表現されたオブジェクトを複製することができます。球の半径やカメラ位置を調整して再度シミュレートしてみるとこのような立体が表示できるようになります。

さらに複雑なフラクタルを
ここまではフレームごとにレイマーチの一ステップを実行し、徐々に立体が浮かび上がるようにしていました。ただしこれではカメラを動かしながらのアニメーションなどができないため、ここからはSimulationエリアをRepeatエリアに置き換えて最初から十分レイが進んだ後の状態を表示することにします。
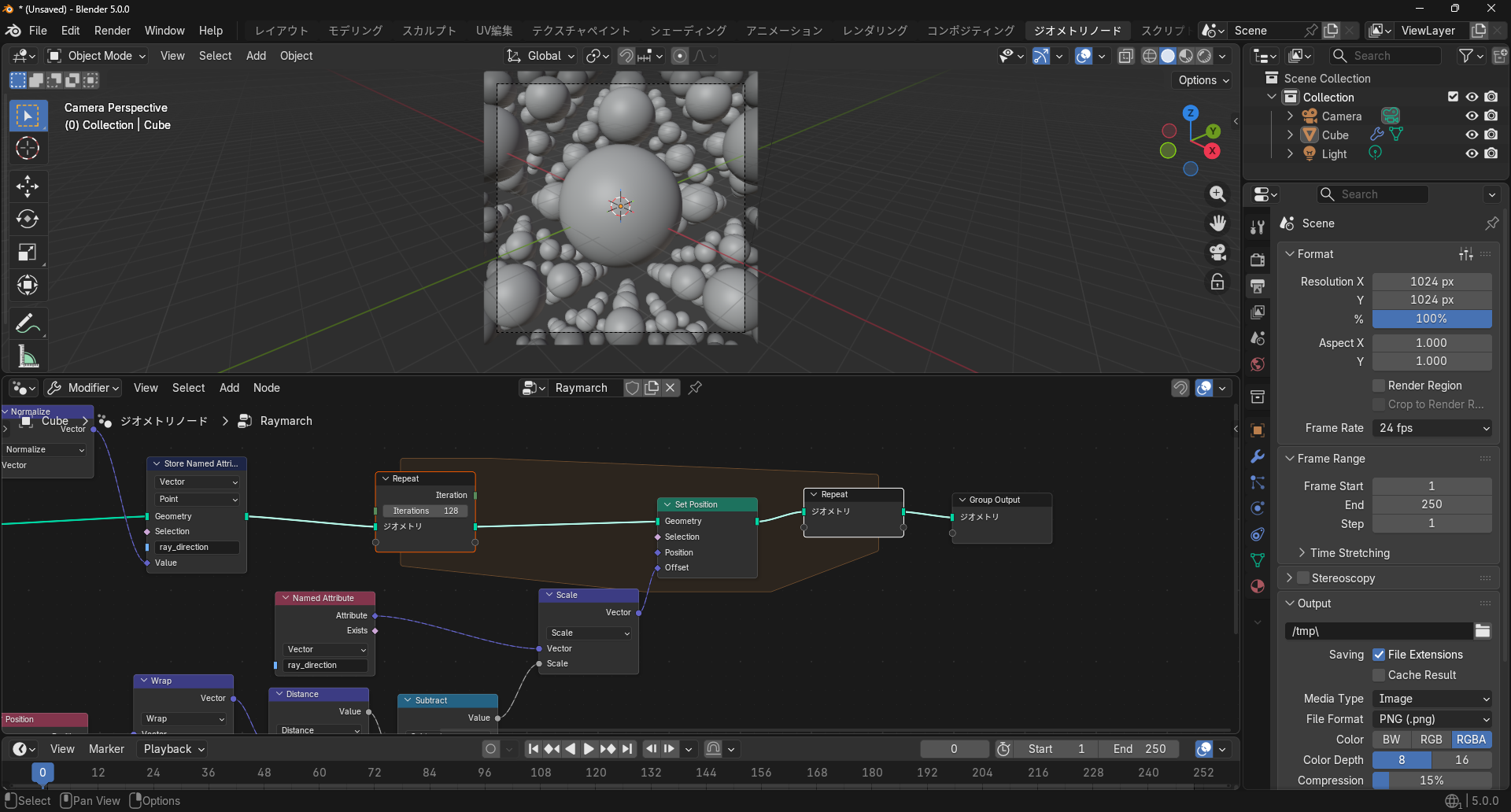
こうして
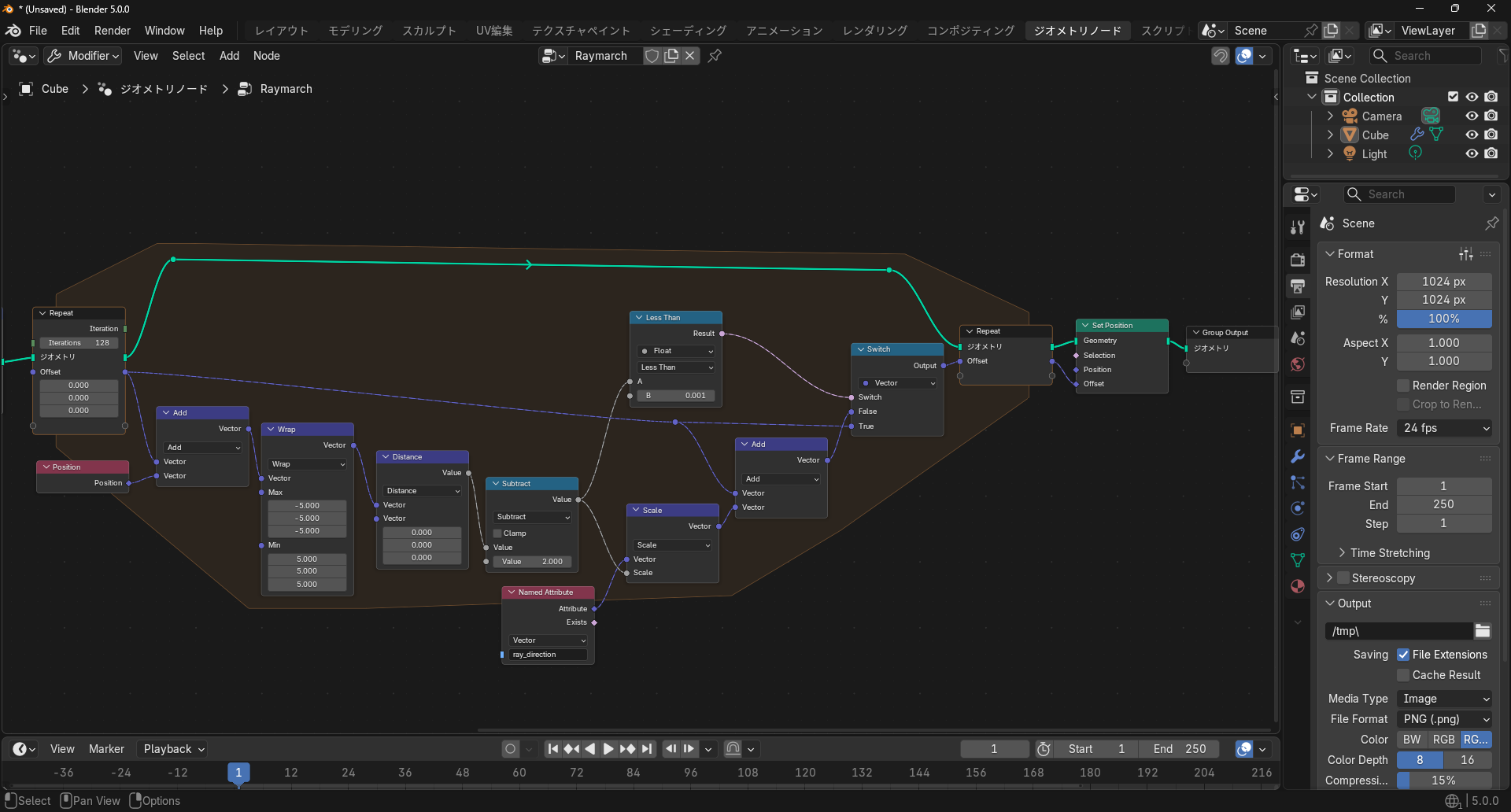
最終的にこうなります。複雑に見えますが、「レイマーチのアルゴリズム」で示したコードをノードで表現した形になっています。(Blender のループは途中で break できないようなので、“条件を満たしたら更新しない”という形で実装しています)
マンデルボックスの距離関数
距離関数の部分を私の一番好きなフラクタル、マンデルボックスで置き換えましょう。 距離関数はmandelbox DEという名前のノードグループにまとめており、mandelbox DEはその中でbox foldとsphere foldを呼び出しています。

mandelbox DE
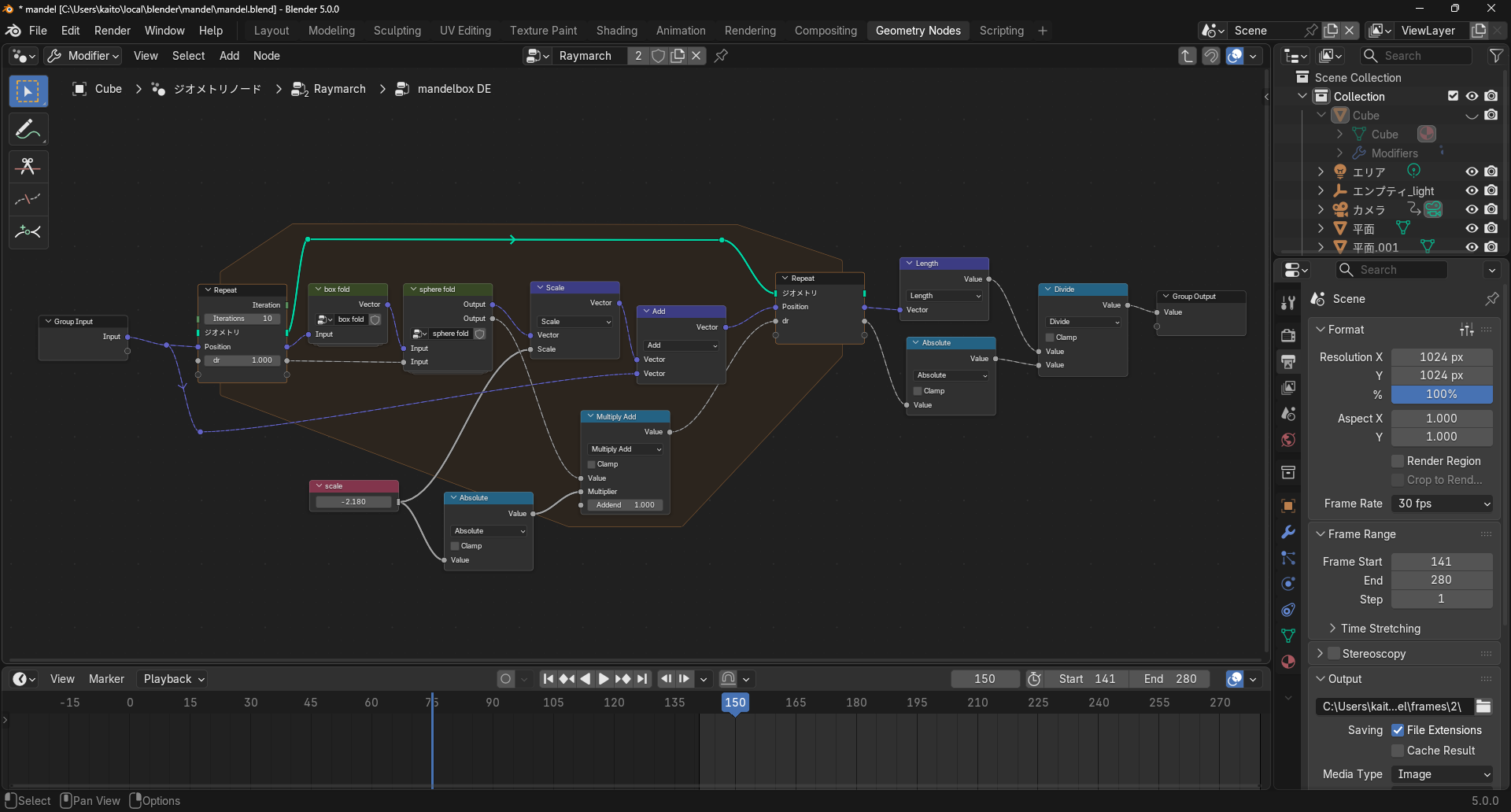
box fold
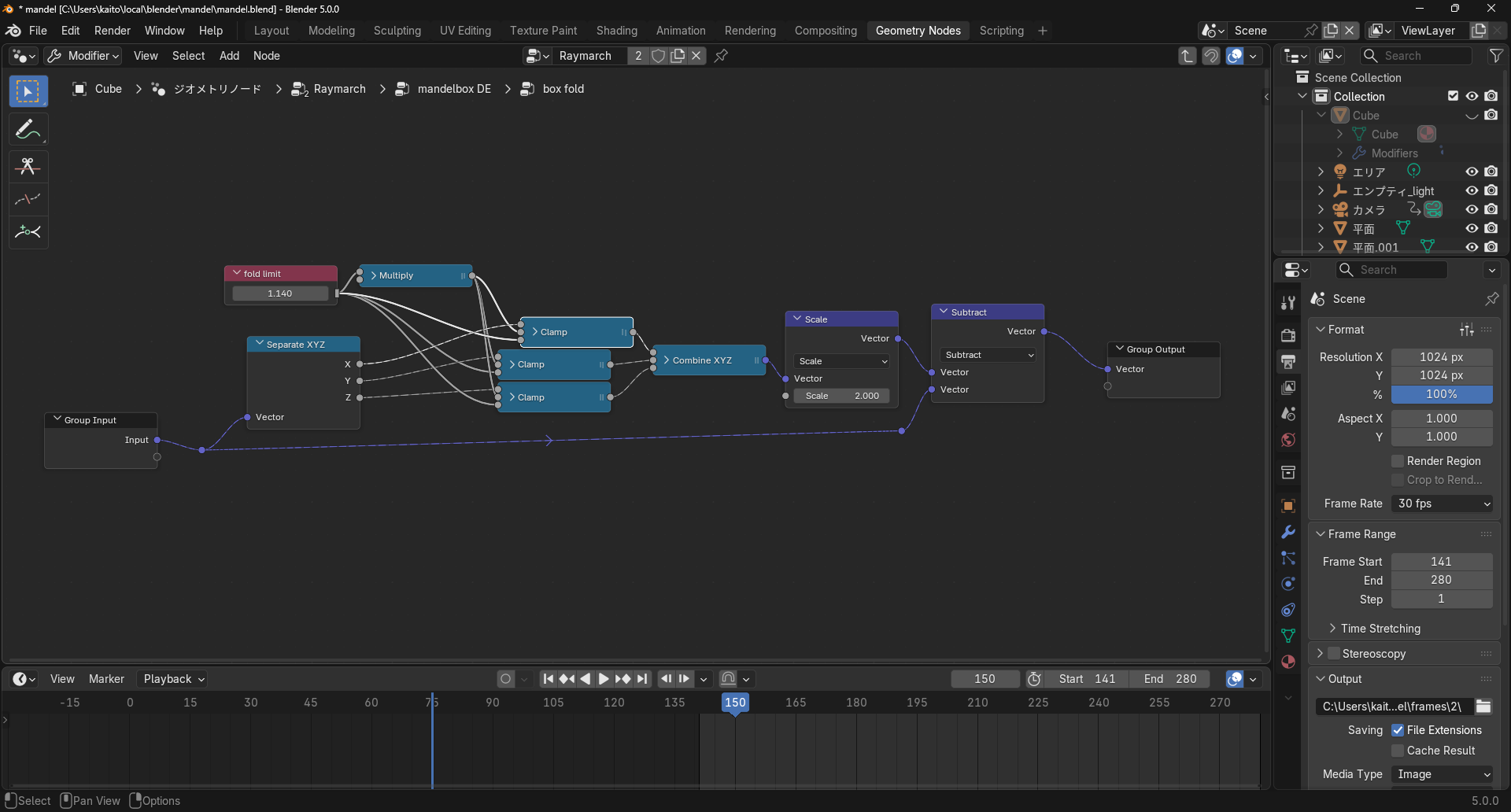
sphere fold

かなり複雑に見えますが、以下のコードをノードで表現したものになっています。
void sphereFold(inout vec3 z, inout float dz) {
float r = length(z);
if (r<0.5) {
// linear inner scaling
float temp =4.0;
z *= temp;
dz*= temp;
} else if (r<1.0) {
// this is the actual sphere inversion
float temp =1.0/(r*r);
z *= temp;
dz*= temp;
}
}
void boxFold(inout vec3 z, inout float dz) {
float foldingLimit=1.0;
z = clamp(z, -foldingLimit, foldingLimit) * 2.0 - z;
}
float mandelboxDE(vec3 z){
float Scale = 2.0;
vec3 offset = z;
float dr = 1.0;
for (int n = 0; n < 32; n++) {
boxFold(z,dr);
sphereFold(z,dr);
z = Scale*z + offset;
dr = dr*abs(Scale)+1.0;
}
float r = length(z);
return r/abs(dr);
}
これでジオメトリノード側の実装はひととおり完了です。こんな感じの立体が表示されるはずです。(とても重いです)
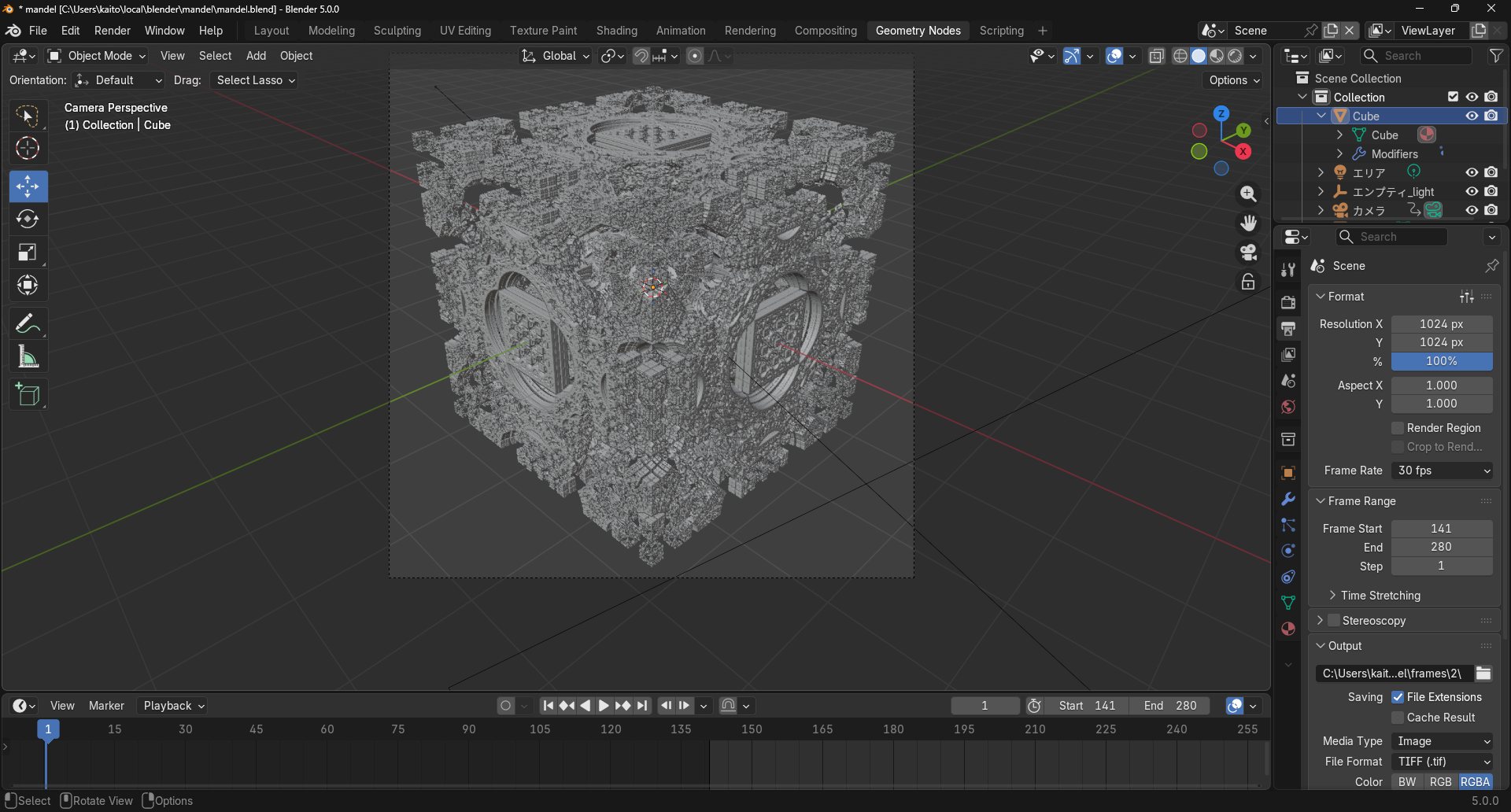
いい感じにする
あとは
- 遠くに飛んで行った頂点をモディファイアで削除する
- 視線に対して水平な平面をモディファイアで削除する
- マテリアルを適用する
- ライティングを追加する
- カメラを移動してアニメーションをつける
などしていい感じにすれば冒頭の動画が出力できます。
感想
というわけで、ジオメトリノードを使ってレイマーチを再現してみました。 実はこれらはシェーダーで実現すればリアルタイムレンダリングできる程度の処理なのですが、 すべてを自分で実装する必要のあるシェーダーブログラミングと違って、Blenderの高度な機能をおのまま利用できるという点は、それを補って余りある利点だと思います。
サブサーフェスマテリアルによって得られる質感や、リッチなUIで編集できるカメラ制御などは表現の幅を大いに広げてくれました。
一方、ノードベースのプログラミングは苦行極まりなく、ノードの配置や面積といった非本質的に頭を悩まされることにもなりました。
自分のセンスではBlenderを使いこなしたと言えるレベルまで演出を洗練させることはかなわず、デモ動画のようなもので精一杯でしたが、是非センスのある人にレイマーチを取り入れた作品を作ってもらいたいですね。
誰かの創作意欲を刺激できたら幸いです。ここまで読んでいただきありがとうございました。


